はじめに
こんにちは!山梨大学工学部コンピュータ理工学科4年の木島です。学生寮「芙蓉寮」に住んでいます。
今回はCS(コンピュータ理工学)の分野をご紹介します。
CSというと最近はAI(人工知能)ばかりが注目されがちですが、AIに直接は関係しないところでも面白い世界は広がっているのです。
ところで、皆さんは以下の数式を見て何か気づくことはありますか?
1/7=0.142857142857…
5/108=0.04629629…
実はこれらは、同じ数字の並びが無限に繰り返される「循環小数」になる割り算です。
人間がこれをみた時、直感的にループしているなと判断するのは簡単です。
では、コンピュータにこのループを見つけさせるには、どうすれば良いでしょうか?
一つの方法は、出てきた数字をすべて記録しておくことです。
過去の記録と比較すればいつかループは見つかります。
しかし、この方法は数字が何万桁も続く場合、記録するためのメモリが膨大になり、確認にも時間がかかってしまいます。
アルゴリズムの紹介
そこで登場するのが、今回ご紹介する「うさぎとかめのアルゴリズム」[1]です。
ここでイソップ寓話の「うさぎとかめ」を思い出してください。足の速いうさぎと、遅いかめが競争するお話です。
このアルゴリズムでは、その特徴をうまく利用します。
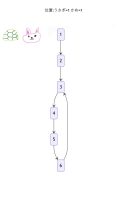
例として、以下のように数字が進むコースを考えます。 1 → 2 → 3 → 4 → 5 → 6 → 4 → 5 → 6 … (1, 2, 3と進んだ後、4, 5, 6の間をぐるぐると回り続けます)
このコースに、うさぎとかめを走らせてみましょう。
以下のルールに従って、うさぎとかめは動きます。
- かめ
- 1回に「1つ」進む
- うさぎ
- 1回に「2つ」進む(かめの2倍の速さ)
それでは、問題を解いていきます。
1.初期位置
うさぎとかめは同時に「1」の地点からスタートします。
2.最初の移動
かめは「2」へ、うさぎは2つ進んで「3」へ行きます。
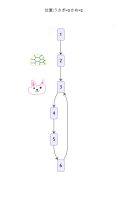
3.次の移動
かめは「3」へ、うさぎは「3」から4→5と進んで「5」へ行きます。
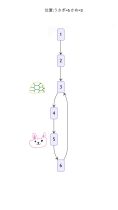
4.その次の移動
かめは「4」へ入ります。 うさぎは「5」から6→4と進んで、なんと「4」へ戻ってきます。
お気づきでしょうか?
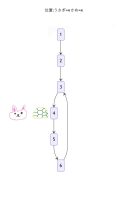
ここで2人は「4」の地点でばったり出会いました。
もしコースが一直線でループしていなければ、足の速いうさぎはかめを置いてきぼりにして、二度と会うことはありません。
しかし、コースがループしている場合、先頭を走るうさぎが周回遅れになって、後ろから来るかめに追いついてしまうのです。
つまり、「2人が出会った=ループが存在する」と判定できるわけです。
これがCSの面白いところです。
「すべての操作を記憶する」という力技ではなく、「速度の違う2つのポインタ」を用意する」という工夫だけで、少ないメモリで高速に問題を解決できるのです。
以下にRust言語で実装した例を示します。
実行した結果が以下の通りです。
範囲内にループがあるかどうかが検出できますね!
まとめ
今回はうさぎとかめのアルゴリズムで、ループが範囲内にあるかどうかを検出する方法について紹介しました。
このアルゴリズム以外でもCS分野には面白い内容が多分に含まれます。
今後もこの様なCS分野の内容を紹介していきたいと思います。
参考文献
[1] Educative.io, “Why does Floyd’s cycle detection algorithm work?,” Educative. [オンライン]. URL<https://www.educative.io/answers/why-does-floyds-cycle-detection-algorithm-work>. [閲覧日:2025-12-07].